Technical Deep-Dive: Anonymous Voting with zk-SNARKs
Discover the technical specifications of Vocdoni's anonymous voting and how we arrived at this design.

This article is a technical deep-dive into our anonymous voting product announcement. You can also try it yourself through vocdoni.app.
Updated documentation can always be found at https://docs.vocdoni.io/architecture/protocol/anonymous-voting/zk-census-proof.html
Defining Anonymous Voting
Before diving into the technical specifications, it's worth mentioning how we define anonymous voting, and why we arrived at this design. In the product announcement article, we introduce two kinds of anonymity: ballot obfuscation and voter anonymity.
Ballot obfuscation refers to anonymity derived from hiding the contents of every vote, whereas voter anonymity severs the link between each voter and their vote, without hiding the votes themselves. Our implementation of anonymous voting uses voter anonymity. Why is this?
Firstly, ballot obfuscation carries with it some significant tradeoffs. To enable end-to-end verifiability of a voting process, voters need to be able to track and examine the contents of the ballots they have cast. If we ensure anonymity with ballot obfuscation, we lose the property of verifiability, as it is impossible to verify that your vote was counted and audit the integrity of the vote if the contents of every vote is hidden.
Another downside to ballot obfuscation is that it is difficult to implement in a digital voting system. One ballot obfuscation technique is the use of homomorphic encryption, which has been proposed to provide cryptographic anonymity to traditional voting systems. Homomorphic encryption enables the computation of encrypted values, meaning a tally of votes can be computed without examining the contents of a single ballot. While sound in theory, homomorphic encryption carries many downsides that make it less desirable as a backbone for voting technology.
Most notably, this method only allows for basic computation of the encrypted ballots, making schemes like quadratic or ranked-choice voting more difficult to implement. Furthermore, while the computation of results is guaranteed with homomorphic encryption, end-to-end verification of a voter’s ballot is not. This scheme provides no cryptographic proof to guarantee a voter’s ballot was included and represented correctly in the set of results. We also estimate that the validation of the homomorphic proof of a voting process would demand significant computational resources, which only scale with larger voting processes. This could negate the benefits of a universally verifiable system, as the verification could only be computed on powerful, expensive machines over a prohibitively long timescale.
Voter anonymity has a number of advantages over homomorphic encryption. Firstly, a much higher degree of end-to-end verifiability is possible. While the link between a voter and their ballot must be opaque to any third-party onlookers, voters themselves can still identify their ballot. Because ballots themselves are visible, therefore, any user can track their vote from the moment it was cast to its inclusion in the results. Furthermore, third parties are able to identify that each ballot belongs to a valid voter and that the contents of this ballot were counted correctly.
Voter anonymity also tends to enable much more computationally efficient designs. Systems with voter anonymity perform obfuscation once on each voter’s ballot proof, rather than on the entire set of results each time a new ballot is cast. No significant computational step is needed to make results widely available. Election results can even be published throughout a voting process without compromising anonymity (given that timing-correlation attacks have been mitigated).
Therefore, we have decided to build voter anonymity into our census proof mechanism.
Census Merkle Tree
The starting point to the voter census mechanism is a census Merkle tree. This is a structure of hashed public keys, each of which represents an eligible voter in a census. The use of a Merkle tree here effectively allows any valid voter to prove that they hold a censusKey, which belongs in the census, without knowing any other voters' keys. The voter then submits this proof as part of their ballot. Also attached to this vote envelope is a nullifier: a piece of data derived from a user's censusKey and the electionID that uniquely corresponds to their vote.
Using this proof alone would allow the organizer of a process to correlate each vote envelope, via its nullifier, with a voter's censusKey, de-anonymizing voting. To combat this, Vocdoni uses zk-SNARKs to ensure voting anonymity.
zk-SNARKs for anonymous voting
zk-SNARK stands for zero-knowledge Succinct Non-interactive ARgument of Knowledge. A zk-SNARK allows a user to prove to a third party that they possess a certain piece of information, without revealing the information itself.
In our case, zk-SNARKs allow voters to prove that they belong in the census without revealing their secretKey. Specifically, this is done with a zk-Circuit, which is a software circuit designed to generate a Zero-Knowledge Proof (ZKP).
zk-Circuit
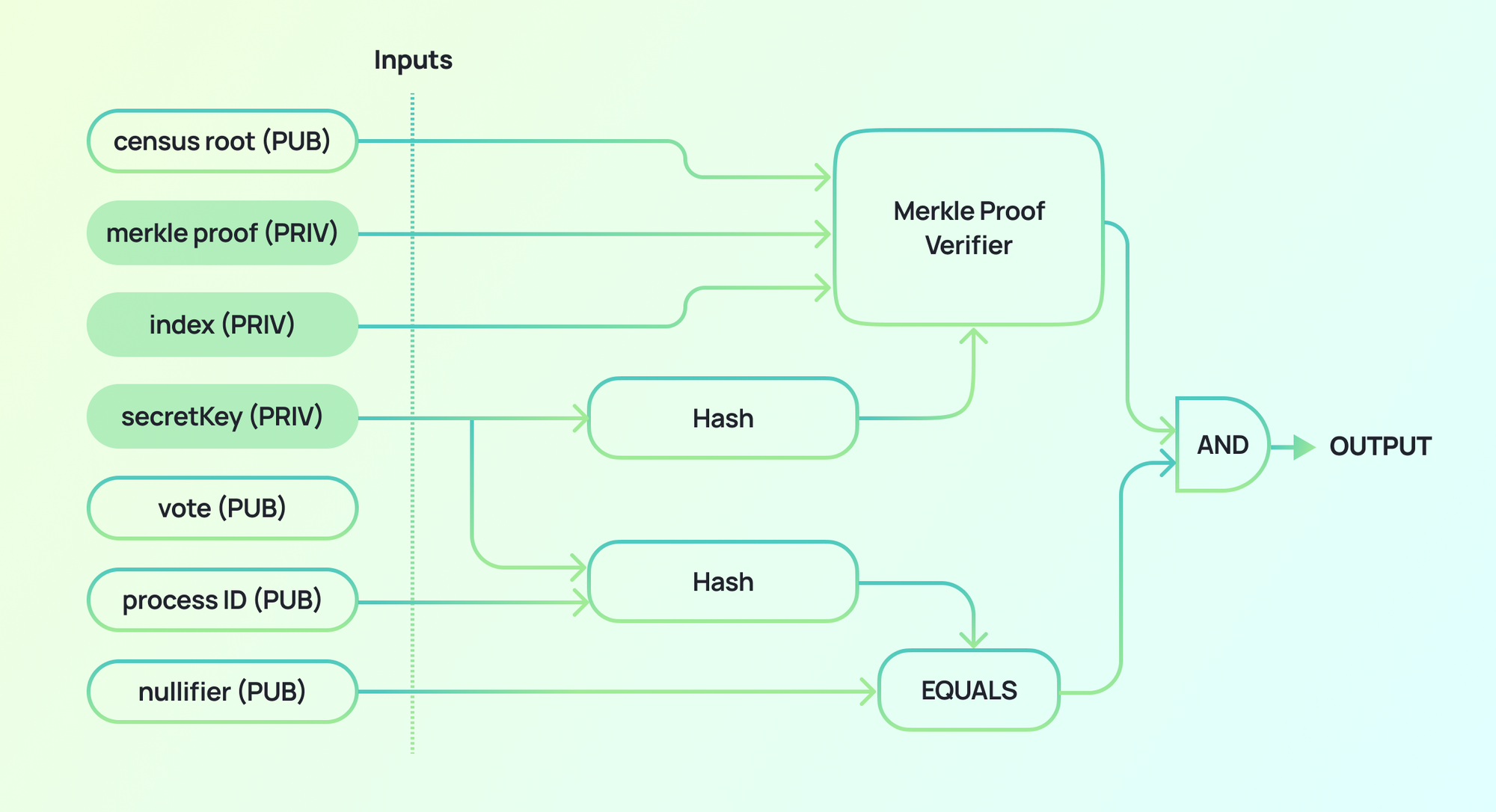
We have designed a circuit that allows users to generate a ZKP of their census membership without revealing their secretKey. The circuit receives both private and public inputs, where data that could reveal the identity of the voter is kept private. Public inputs are submitted within the vote envelope so that validators can check them against the proof and make sure that the user hasn't voted twice.
The circuit can be used for any process with a census of a similar size, and only needs to be generated once per size. To be more specific, a circuit can be generated and then reused for any census Merkle tree with the same tree height. Since we use a binary tree, this means one circuit is needed for each value n where the target census size is within the range of 2^n(eg. 128, 256, ..., 8192, 16384, etc).
Circuit generation relies on a trusted setup ceremony. This is a process for generating the prover and verifier keys for the circuit, and it is “trusted” because, if one party controls the entire generation of these keys, they could generate false proofs. Therefore, a decentralized ‘ceremony’ is needed to ensure the reliability of the circuit. In such a ceremony, various parties with conflicting interests and in different locations each perform one step of the key generation. If only one of these parties maintains integrity, it will be impossible to generate a false proof.
The franchise proof is generated by running the zk-SNARK circuit.
- Private inputs:
index,secretKey,census Merkle-proof - Public inputs:
census Merkle-root,nullifier,election ID,vote - Output:
franchise proof
Defining Anonymous Voting
Before diving into the technical specifications, it's worth mentioning how we define anonymous voting, and why we arrived at this design. In the product announcement article, we introduce two kinds of anonymity: ballot obfuscation and voter anonymity.
Ballot obfuscation refers to anonymity derived from hiding the contents of every vote, whereas voter anonymity severs the link between each voter and their vote, without hiding the votes themselves. Our implementation of anonymous voting uses voter anonymity. Why is this?
Firstly, ballot obfuscation carries with it some significant tradeoffs. To enable end-to-end verifiability of a voting process, voters need to be able to track and examine the contents of the ballots they have cast. If we ensure anonymity with ballot obfuscation, we lose the property of verifiability, as it is impossible to verify that your vote was counted and audit the integrity of the vote if the contents of every vote is hidden.
Another downside to ballot obfuscation is that it is difficult to implement in a digital voting system. One ballot obfuscation technique is the use of homomorphic encryption, which has been proposed to provide cryptographic anonymity to traditional voting systems. Homomorphic encryption enables the computation of encrypted values, meaning a tally of votes can be computed without examining the contents of a single ballot. While sound in theory, homomorphic encryption carries many downsides that make it less desirable as a backbone for voting technology.
Most notably, this method only allows for basic computation of the encrypted ballots, making schemes like quadratic or ranked-choice voting more difficult to implement. Furthermore, while the computation of results is guaranteed with homomorphic encryption, end-to-end verification of a voter’s ballot is not. This scheme provides no cryptographic proof to guarantee a voter’s ballot was included and represented correctly in the set of results. We also estimate that the validation of the homomorphic proof of a voting process would demand significant computational resources, which only scale with larger voting processes. This could negate the benefits of a universally verifiable system, as the verification could only be computed on powerful, expensive machines over a prohibitively long timescale.
Voter anonymity has a number of advantages over homomorphic encryption. Firstly, a much higher degree of end-to-end verifiability is possible. While the link between a voter and their ballot must be opaque to any third-party onlookers, voters themselves can still identify their ballot. Because ballots themselves are visible, therefore, any user can track their vote from the moment it was cast to its inclusion in the results. Furthermore, third parties are able to identify that each ballot belongs to a valid voter and that the contents of this ballot were counted correctly.
Voter anonymity also tends to enable much more computationally efficient designs. Systems with voter anonymity perform obfuscation once on each voter’s ballot proof, rather than on the entire set of results each time a new ballot is cast. No significant computational step is needed to make results widely available. Election results can even be published throughout a voting process without compromising anonymity (given that timing-correlation attacks have been mitigated).
Therefore, we have decided to build voter anonymity into our census proof mechanism.
Census Merkle Tree
The starting point to the voter census mechanism is a census Merkle tree. This is a structure of hashed public keys, each of which represents an eligible voter in a census. The use of a Merkle tree here effectively allows any valid voter to prove that they hold a censusKey, which belongs in the census, without knowing any other voters' keys. The voter then submits this proof as part of their ballot. Also attached to this vote envelope is a nullifier: a piece of data derived from a user's censusKey and the electionID that uniquely corresponds to their vote.
Using this proof alone would allow the organizer of a process to correlate each vote envelope, via its nullifier, with a voter's censusKey, de-anonymizing voting. To combat this, Vocdoni uses zk-SNARKs to ensure voting anonymity.
zk-SNARKs for anonymous voting
zk-SNARK stands for zero-knowledge Succinct Non-interactive ARgument of Knowledge. A zk-SNARK allows a user to prove to a third party that they possess a certain piece of information, without revealing the information itself.
In our case, zk-SNARKs allow voters to prove that they belong in the census without revealing their secretKey. Specifically, this is done with a zk-Circuit, which is a software circuit designed to generate a Zero-Knowledge Proof (ZKP).
zk-Circuit
We have designed a circuit that allows users to generate a ZKP of their census membership without revealing their secretKey. The circuit receives both private and public inputs, where data that could reveal the identity of the voter is kept private. Public inputs are submitted within the vote envelope so that validators can check them against the proof and make sure that the user hasn't voted twice.
The circuit can be used for any process with a census of a similar size, and only needs to be generated once per size. To be more specific, a circuit can be generated and then reused for any census Merkle tree with the same tree height. Since we use a binary tree, this means one circuit is needed for each value n where the target census size is within the range of 2^n(eg. 128, 256, ..., 8192, 16384, etc).
Circuit generation relies on a trusted setup ceremony. This is a process for generating the prover and verifier keys for the circuit, and it is “trusted” because, if one party controls the entire generation of these keys, they could generate false proofs. Therefore, a decentralized ‘ceremony’ is needed to ensure the reliability of the circuit. In such a ceremony, various parties with conflicting interests and in different locations each perform one step of the key generation. If only one of these parties maintains integrity, it will be impossible to generate a false proof.
The franchise proof is generated by running the zk-SNARK circuit.
- Private inputs:
index,secretKey,census Merkle-proof - Public inputs:
census Merkle-root,nullifier,election ID,vote - Output:
franchise proof

Without revealing the secretKey or Census Merkle Proof, this circuit is able to demonstrate that:
- The voter is the owner of the
secretKeycorresponding to a certainzkCensusKey. - The voter's
zkCensusKeyis included in the census Merkle tree. - The
nullifierprovided by the voter uniquely corresponds to theirsecretKeyand theelection IDfor a specific voting process.
Although the computation is CPU- and memory-intensive, ZKPs can be generated from the user client, running on modest hardware. In the Vocdoni protocol, the proof is validated by the Vochain nodes, miners, and any third party monitoring the process.
The Circuit is minimized and optimized to its minimum requirements in order to make it accessible for any kind of client hardware. This is the reason behind not using signature verification but a secretKey approach instead.
Merkle & census trees
The Merkle tree used for building the anonymous census needs to be a zk-SNARK-friendly implementation. As we currently use the Circom compiler for the zk-SNARK circuits, we need a tree that is compatible with the circomlib Merkle tree implementation. A specification of such a Merkle tree can be found here.
Vochain uses the arbo Merkle tree, a Go implementation compatible with the Circom design. The Merkle tree uses the Poseidon Hash, a 'SNARK-friendly' hash function that can later be proved inside a circuit without requiring too many constraints. The following diagram is a visual representation of the data structure of the leaves on the Merkle tree being used in the scheme of the zk-census-proof.
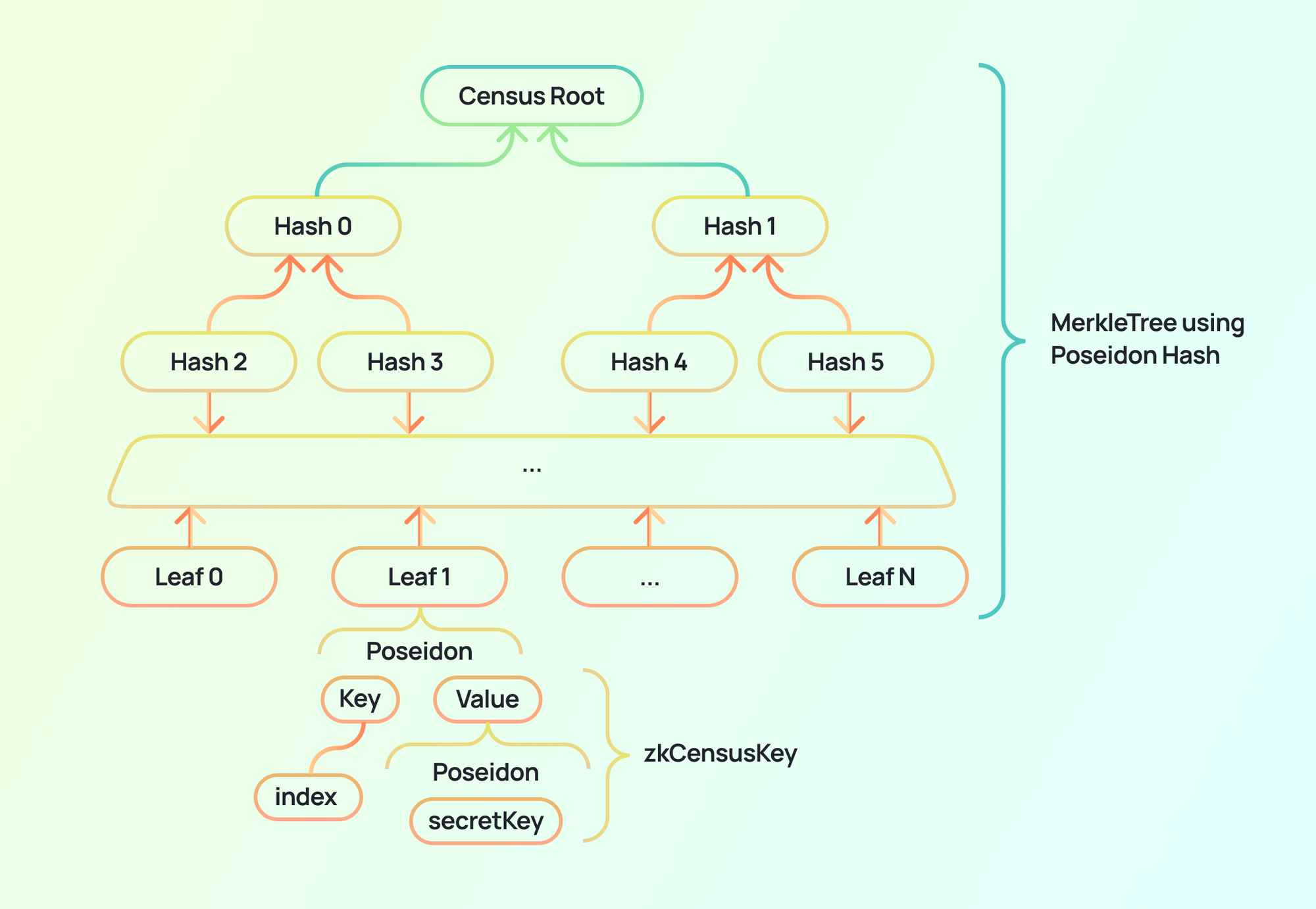
The index value is determined by the census tree builder, which has an index value for each census tree. This value increments with the addition of each new leaf. The leaves are structured in this way in order to use the Merkle trees more efficiently, allowing more users’ keys to fit inside a smaller tree, thereby reducing the zk-Circuit size. This is because the value of any given leaf's key determines that leaf's position on the tree.
If the leaf’s key were determined by the zkCensusKey, rather than an incremental index, each new leaf would have a significant chance of collision before filling all the available leaf spots for a given height. Trees would therefore be less balanced and would require larger circuits for the same census size due to inefficient use of tree space. With the incremental index approach, on the other hand, all the leaf spots can be filled without a single collision. This produces much smaller circuits for the same number of users.
zk-Inputs generation
{
"censusRoot": "51642541620950251760298704744678482162425252475654827255045491135352807540162",
"censusSiblings": ["0","0","0","0"],
"index": "30",
"secretKey": "6190793965647866647574058687473278714480561351424348391693421151024369116465",
"voteValue": ["100964581237483263846637432502620436451", "278307331411790712608582894981321409946"],
"electionId": "10",
"nullifier": "1938187656076799017313903315498318464349291455761501098436114043715056719301",
}
Origin of each zk-Input parameter:
All the parameters are string or []string that represent bigInt or []bigInt.
censusRoot: computed by the census authority from the census tree.censusSiblings: computed by the census authority; is the Merkle proof- the user retrieves the siblings from the Vochain through the gateway.
- the length of
censusSiblingswill depend on the zk-Circuit: - The design of the Merkle tree used in circomlib provokes different lengths in the siblings to be returned when generating a Merkle proof.
- The depth of the tree, as defined from the root to the leaves, will depend on each leaf and its neighbors.
- More details can be found in the Merkle tree spec.
- In order to input those siblings into the circuit, the
nLevelsof the circuit is fixed, sosiblings.lengthneeds to be fixed as well. - The
siblings.lengthwill depend on the zk-Circuit being used, specifically from thenLevelsparameter of the circuit - The logic needed to be implemented in the user side can be found here (go) lines 67-70, and here (js) line 23:
while (siblings.length < this.levels) siblings.push(BigInt(0)); index: determined by the Vochain when adding the user'szkCensusKeyinto the census treesecretKey: generated by the uservoteValue: hashed value of the user vote, composed by two big integers.- The raw user vote is a variable-length array of values and its values do not need to be checked in the circuit. Furthermore, the values can be encrypted.
- Since the encoded vote values may not fit into a constant number of circuit inputs, we calculate a summary of the raw user vote using an EVM-friendly hash function:
sha256(vote_bytes). The output of thesha256hash is slightly larger than the field used in SNARKS, so we split the hash output (32-bytes) into 2 16-byte arrays, take them as integers (in little-endian), and use them as circuit inputs. sha256hash is used, as if necessary in the future it can be verified inside the circuit. This usage has two characteristics to keep in mind:sha256is twice as expensive askeccak256in terms of gas in EVM, but it is implemented in circom, so it can be checked inside a circuit checking thesha256inside a circom circuit is expensive in terms of number of constraints (in the current version of this spec, this is not checked inside the circuit).
h := sha256.Sum256(voteBytes) // voteBytes can be the votes array converted to bytes, or the encrypted votes
b1 := new(big.Int).SetBytes(swapEndianness(h[:16])) // swap endianness, as golang big int package works in big-endian, and we use little-endian
b2 := new(big.Int).SetBytes(swapEndianness(h[16:]))
And the json input of the voteValue for the circuit would be: "voteValue": [b1, b2]
electionID: the election ID in which the user is participatingnullifier: computed by usernullifier = poseidon.Hash(sk, electionID)
Anonymous voting for DAOs
To answer the question “how can this technology be used for Ethereum DAO voting”, we need to add some context:
- Currently, Ethereum's internal cryptography, data structures, and merkle tree are not zk-SNARK friendly, so the options are limited (for now).
- Vocdoni currently supports Ethereum storage proof voting which is the current more secure and trustless way to execute gasless offchain voting (implemented in https://voice.aragon.org frontend)
- While Vocdoni does not yet provide full offchain binding execution (voting within Ethereum requires an optimistic approach), we have done some proof-of-concept work on this scope, and we are continuing to research to achieve full properties (new designs and proof-of-concepts coming soon).
The way Vocdoni can currently support voting anonymously on DAOs is by following the next steps:
- A new election is created in the Vocdoni blockchain with censusRoot equal to the Ethereum state root and the ERC20 contract address.
- Users fetch an Ethereum storage proof from Web3 that demonstrates they hold tokens for a contract and a state root.
- Users generate a new temporary
secretKeyand send a transaction to the Vocdoni blockchain, proving they are eligible voters (by using the storage proof). This transaction includes the hashedsecretKeywhich is added to arolling Censuswhich is computed internally by the Vocdoni blockchain logic. This step is named key pre-register. - Once the pre-register is finished, users can anonymously vote using their
secretKey
